Three-phase motors in single-phase operation

 

Three-phase motors can also be operated with single-phase alternating voltage. A time shift in the current in one winding strand is normally achieved using an operating capacitor. This in turn causes a magnetic field to be generated. However, due to the capacitor the currents flowing in the windings are not all of equal magnitude. The rotating field is no longer circular but has an elliptical shape. This leads to a considerable drop in power and starting torque.

Two winding motor

Two winding motor Design

Most single-phase induction motors are designed as dual-winding machines. In contrast to single-phase motors there are two separate winding phases built into the stator of the two-phase motor – the power winding and the auxiliary winding. The auxiliary winding is normally disconnected after the motor has successfully started. The auxiliary winding coils are laid between the coils of the power winding. A squirrel-cage rotor is used as a rotor.

Direction of magnetic fields

 

If you connect the main winding to an AC voltage, the motor responds like a transformer with a short-circuited secondary winding. If the rotor had been purely inductive, the magnetic fields in the stator and rotor would have been phase-shifted by 180°. However, due to the fact that the rotor impedance also contains a resistive component, the north pole of the rotor field is always 15° behind the south pole of the stator field. This means that a torque cannot be generated when the motor is switched on.

Types of induction motors with squirrel-cage rotors

 

The starting torque can be produced with the aid of a rotating magnetic field. The prerequisite for this is a phase-shift between the currents flowing in the working and auxiliary windings which are situated at 90° to one another. The phase-shifted voltage feed of the auxiliary winding can be achieved either through an equivalent resistance, a capacitor or a choke. Depending on the circuitry used for the phase shift, a distinction can be drawn between five different types of two-phased asynchronous motors.

How the motor works

The phase shift between the currents in the two stator windings is achieved in this motor by implementing a considerable amount of active resistance in the auxiliary winding. The auxiliary winding comprises either a larger number of winding turns, lower wire cross-section or is made of resistive material. If the current in the auxiliary winding leads the current in the power winding, the rotation direction is from the pole of the auxiliary winding to the next pole of the power winding. After start-up the auxiliary winding is normally disconnected using a centrifugal switch or a current relay.

Operating characteristics

 

It is the asymmetrical rotating field which is responsible for the motor's relatively low torque during starting. The starting current amounts to approximately six times the rated current, while the starting torque is about equal to the rated torque. After the auxiliary winding is disconnected, the motor demonstrates the characteristics of single-winding single-phase motors. For that reason such motors are nowadays manufactured exclusively with power levels of under 1 kW and used where they do not need frequent starting.

Capacitro motor with starting capacitor

A capacitor is connected in series with the auxiliary winding. It is selected so that, in phase terms, the current in this winding is ahead of the applied voltage by 40°. The inductance of the power winding is the reason for the fact that current in this winding lags the voltage by 50°. The result of this is a 90° phase shift between the winding currents. When 75% of the nominal speed is reached the auxiliary winding is disconnected from the capacitor. Because the small electrolytic capacitor is only in operation for a few seconds, its value can be chosen to be adequately large – around 200 µF.

Operating response

 

Capacitor motors with starting capacitors are the most popular single-phase AC motors in use. Their starting characteristics are better than those for motors with resistive auxiliary phase windings. The starting torque is higher, the starting current consumed is lower and the power factor is better. After the auxiliary winding is disconnected, the motor demonstrates the operational characteristics of single-winding single-phase motors.

Asynchronous motor

Induction motors with squirrel-cage rotors

 

In the repulsion motor the collector and brushes are only used in the starting phase. After a certain speed has been attained the rotor is short-circuited. The next logical step in the simplification of its construction is the short-circuit rotor, usually referred to as a squirrel-cage. The single-phase asynchronous machines have the same simple mechanical design as three-phase motors. A distinction is drawn between single-phase and two-phase motors depending on the number of phase windings.

Design

This motor has a particularly simple and straight-forward design. The laminated stator is equipped with a power winding taking up 2/3 of the grooves. The squirrel-cage consists of two short-circuit rings, which are interconnected by aluminium or copper bars running close beneath the surface of the rotor core. In order to keep power losses low, a deep-bar rotor is not used. The grooves can take a variety of forms.

Direction of the magnetic fields

 

 If the power winding is connected to an alternating voltage, the motor responds like a transformer with short-circuited secondary winding. There is a 180° phase shift between the magnetic fields in the stator and rotor – the fields oppose each other and there is no starting torque generated when the motor is switched on.

How it works

 

The pulsating alternating field in the stator can be perceived as two magnetic fields rotating in opposite directions, which at standsill build up two torques of opposite and equal magnitude. The resulting torque is equal to zero. The hand-operated pony motor does not start by itself – it must be cranked in one direction or the other. After start-up, one of the partial moments will predominate so that the resulting torque becomes greater than zero – the motor accelerates until it reaches its rated speed. Here the same regularities and functional principles apply as elaborated on in the section on the repulsion motor.

 

Operating attributes

 

Compared to other motor types the hand-operated single-phase motor (pony) demonstrates a number of negative characteristics.
Pony motors are only used for small concrete mixers or grinding machines.

 

Repulsion Motor

Design of Repulsion Motor

The repulsion motor is the first single-phase AC motor in which the armature field builds up as a consequence of the voltage induced in the rotor. The rotor has the same design as the one in the universal motor – laminated sheet steel with an armature winding inserted into grooves, whose coil ends are connected to the collector segments. The carbon brushes no longer serve to feed current – they are attached on a moveable mount and short-circuited. The stator has no salient pole pieces – the exciter winding is inserted into the grooves of the dynamo steel core.

How the motor works

 

As was the case in the transformer the current carrying exciter winding induces a voltage in the coils of the armature winding. The position of the short-circuited brushes determines the current flow in the armature winding. If the brushes are aligned with the magnetic poles, the total current is equal to 0 – no magnetic field can build up in the rotor. The maximum current flows through the armature winding when the brushes are rotated by 90° from this alignment. A magnetic field arises whose direction coincides with the direction of the magnetic field in the stator. These brush positions are correspondingly defined as the "soft" and "hard" neutral positions.

Torque, speed and back emf

In order for torque to be exerted on the rotor, the brushes are turned by 15° out of the "hard" neutral position. Now the north pole of the rotor is repelled by the north pole of the stator. If the brushes are turned by 15° in the opposite direction, the rotation direction of the motor is reversed. At approx. 75% of the rated speed all of the collector segments are short-circuited with a ring and the brushes are lifted – their position no longer determines the amplitude of the armature current. Only the induced back emf is responsible for the armature current in the short-circuited rotor.

Short-circuit voltage and current

 

The output voltage of the transformer depends on the type of load and on the load current. One measure for voltage change is the short-circuit voltage, which is the voltage that must be applied to the input winding so that it consumes the rated current when the output winding is short-circuited. In transformers with low internal resistance the output voltage only drops off slightly under load. This kind of transformer has a rigid voltage characteristic. Transformers with high short-circuit voltage are called voltage compliant or flexible. Critical for the short-circuit response is the dispersion which differs for various winding arrangements.

Power dissipation and efficiency

 

The efficiency of transformers is specified as the ratio between active power output and absorbed active power. Transformation of electrical energy in real transformers involves power loss. This includes the load-dependent losses in the winding impedance, as well as the voltage and frequency dependent magnetic and eddy current losses arising in the magnetic circuit. The power loss is converted into thermal energy. The iron losses are measured in no-load operation whereas the winding losses are measured in short-circuit experiments.

Operation at no-load and under load

 

Without load the transformer responds like a coil of large inductance. The current consumed by the input winding is the no-load current. The no-load voltage induced at the output is computed according to the primary transformer equation. When operating at no-load almost all of the magnetic flux is concentrated in the iron core. When a load is connected, the load current weakens the input current in accordance with Lenz's law. Some of the lines of flux are then distributed outside the core and this is called leakage flux.

Transformation ratios

 

In an ideal transformer which achieves 100% power coupling (loss-free) the same magnetic flux permeates both windings. Without load the voltages respond in line with the number of winding turns. The higher to lower voltage ratio is called the transformation ratio. When the transformer is coupled the currents under load respond in inverse ratio to the number of turns. The impedances are carried forward in the square of the transformation ratio. Due to the power losses arising in real transformers these transformation ratios are only approximately correct.

Types of Inductors

 

An inductor is basically a coil of wire. The material around which the coil is formed is called the core. Both fixed and variable inductors are classified according to the type of core material used. Three common types are: the air core, the iron core, and the ferrite core. Each has a unique symbol, shown above. Inductors are made in a variety of shapes and sizes. Some are shown above. Small fixed inductors are encapsulated in an insulating material and have the appearance of a small resistor. Variable inductors usually have a screw type adjustment, to allow inductance to be changed. 

Series and Parallel Inductors

When inductors are connected in series, the total inductance, L_T, is the sum of the individual inductors. The formula is similar to total resistance in series and total capacitance in parallel.

 

When inductors are connected in parallel the total inductance is less than the smallest inductance. The reciprocal of the total inductance is equal to the sum of the reciprocals of the individual inductances. The formula is similar to the formula for total parallel resistance and total series capacitance.

Lenz's Law

 

When the current through a coil changes, a voltage is induced. Lenz's Law states that the polarity of the induced voltage always opposes the change in current that caused it. The diagram above illustrates this law. When the switch closes, the current tries to increase, and the magnetic field starts expanding. The expanding magnetic field induces a voltage, which opposes an increase in current. So, at the instant of switching, the current remains the same. When the rate of expansion decreases, the induced voltage decreases, allowing the current to increase. As the current reaches a constant value, there is no induced voltage.  

The diagram illustrates the direction of induced voltage when the current is switched off. In a steady-state condition, the current has a constant value. There is no induced voltage because the magnetic field is unchanging. If the switch is opened, the current tries to reduce, and the magnetic field begins to collapse. At the time of switching, the induced voltage has a direction that prevents any decrease in current. The current remains the same as prior to the switch opening. When the rate of collapse decreases, induced voltage decreases, allowing current to decrease to zero value. 

Inductor

Faraday's Law

A permanent magnet has a magnetic field around it, which consists of lines of force, or flux lines Φ, going from the north pole (N) to the south pole (S). Moving a magnet relative to a coil of wire and thus cutting across the flux lines induces a current through the coil.

 

Faraday's Law states: The induced voltage u_ind is directly proportional to the rate of change of the magnetic field with respect to the coil and the number of turns in the coil. A coil with more turns (loops), produces a greater voltage. The faster the magnet is moved, the greater the induced voltage.

Basic Inductor

 

A coil of wire forms a basic inductor. Current through the coil produces an electromagnetic field, which creates a north (N) and a south (S) pole. The more lines of force, the greater the flux, and the stronger the magnetic field.
Constant current has an associated constant magnetic field and there is no induced voltage. An increase in current expands the field. A decrease in current reduces it. As the field expands and collapses with current change, the flux Φ is effectively in motion. Hence, a varying current can produce induced voltage without magnetic motion.

Inductance

 

Inductance is the ability of a conductor to produce induced voltage when the current varies. Conductors that introduce a definite inductance into the circuit are called inductors or coils. The symbol for inductance is L, and the unit is the Henry (H). The inductance is one Henry when the current, changing at the rate of 1A per second, induces 1V across the coil.

An inductor stores energy in the magnetic field created by the current. The energy stored is proportional to the inductance and the square of the current. The energy is supplied by the voltage source that produces the current.

More Detail about Inductor

RC Circuit

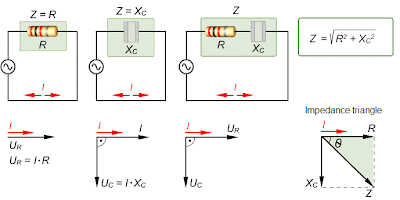
Series RC Circuit

In a series RC circuit, the current is the same through both the resistor and capacitor. Thus, the resistor voltage (U_R) is in phase with the current (I), and the capacitor voltage (U_C) lags the current by 90^o. Therefore, there is a phase difference of 90^o between U_R and U_C as shown above. From Kirchoff's voltage law, the sum of the voltage drops must equal the source voltage, U_s. Since U_R and U_C are 90^o out of phase, the magnitude of the source voltage can be expressed by using the Pythagorean theorem, as shown in the diagram.

Capacitive Impedance

The impedance Z of an RC circuit is the complete opposite to sinusoidal current. Its unit is the ohm. The phase angle is the phase difference between the total current and the source voltage. In a purely resistive circuit, the impedance is equal to total resistance. The phase angle is zero. In a purely capacitive circuit, the impedance is the total capacitive reactance. The phase angle is 90^o, with the current leading the voltage. The impedance, Z, of a series RC circuit, depends on both the R and the C reactance values. It is determined by the impedance triangle shown. The phase angle is between zero and 90^o.

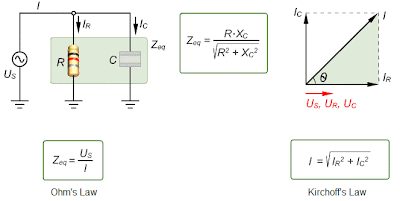
Z_C Frequency Dependence

 

Capacitance reactance X_c varies inversely with frequency. Impedance Z changes in the same way as X_c. Therefore, in RC circuits, Z is inversely related to frequency. The diagram illustrates how Z and X_c change with frequency, with the source voltage held at a constant value. As the frequency increases, X_c decreases. Less voltage is dropped across the capacitor since U_c = I X_c. Also, Z decreases as X_c decreases, causing the current to increase. An increase in I causes more voltage across R as U_R = IR

 

Analysis of RC Circuit

Analysis of Series RC Circuit

 

Ohm's Law and Kirchoff's Law are used in the analysis of a series RC circuit. Ohm's Law, when applied to a series RC circuit, involves the use of quantities of Z, U, and I. The three equivalent forms of Ohm's Law are shown above. From Kirchoff's voltage law, the sum of the voltage drops equals the source voltage (U_s). Since U_R and U_C are 90^o out of phase, the magnitude of the source voltage is expressed by the voltage triangle as shown in the illustration.  

Analysis of Parallel RC Circuit

 

The source voltage appears across both the resistive and the capacitive branches. Therefore, U_s, U_R and U_c are all in phase and of the same magnitude. In a parallel circuit, each branch has its individual current. The resistive branch current I_R is in phase with U_s, but the capacitive branch current I_c leads U_s by 90^o. By Kirchoff's current law, the total current is the phasor sum of the two branch currents. The impedance of a parallel circuit equals the applied voltage divided by the total current Z_eq = U_s / I. 

 

Capacitors in DC Circuit

Capacitors in DC Circuit (Charging)

Charging and discharging are the main effects of capacitors. A capacitor charges when it is connected to a DC voltage source through a resistor. Initially, when the switch is open, there is no voltage flowing across the capacitor's plate. When the switch is closed, the current jumps to its maximum value, and the capacitor begins to charge. As the charging process continues, the current decreases, and the voltage across the capacitor increases until it equals the source voltage. When the capacitor is fully charged, there is no current. A capacitor blocks constant DC. A capacitor charges following a nonlinear curve as shown above.

Capacitors in DC Circuit (Discharging)

 

The capacitor discharges when a conducting path is provided across the plates without any applied voltage. A capacitor can serve as a voltage source, temporarily, by producing a discharge current. When the switch is closed, the capacitor begins to discharge. Initially, the current jumps to a maximum. The direction of the current during discharge is opposite to that of the charging current. During discharging, the current and capacitor voltages decrease. When the capacitor has fully discharged, the current and the capacitor voltage are zero. The discharging curve is shown in the illustration above.  

RC Time Constant

A certain time is required for the capacitor to fully charge or discharge. The rate at which the capacitor charges or discharges is determined by the RC time constant of the circuit. It is symbolized by Greek letter τ (Tau), where τ = RC. When R is increased, the charging current is reduced, thus increasing the charging time of the capacitor. When C is increased, the amount of charge increases, thus, more time is required to charge capacitor for the same current. In one time constant, the capacitor voltage changes approximately 63%. It reaches its final value at approximately 5τ.

Series & Parallel Capacitors

Series Capacitors

When the capacitors are connected in series, the total capacitance is less than the smallest capacitance value.

Both capacitors store the same amount of charge. The voltage across each one depends on its capacitance value (U = Q/C). By Kirchoff's voltage law, the sum of the capacitor voltages equals the source voltage (U_s = U₁ + U₂). Since U = Q/C and Q = Q_T = Q₁ = Q₂ the relationship for two capacitors in series is derived. It can be extended to any number of capacitors in series as shown in the diagram. 

Parallel Capacitors

When capacitors are connected in parallel, the total capacitance is the sum of the individual capacitances. When the switch is closed, part of the total charge is stored by C₁ and part is stored by C₂. The portion of the total charge that is stored by each capacitor depends on its capacitance value (Q = CU). Since the voltage across both capacitors is the same, the larger capacitor stores more charge. The charges stored by both capacitors equals the total charge that was delivered from the source (Q_T = Q₁ + Q₂). Because all the voltages are the same, the C_T is the sum of both capacitances.

Capacitor in AC Circuit

The most important property of a capacitor is its ability to block a steady DC voltage, while passing AC signals.

 

In the illustration above, the capacitor is connected to a sinusoidal voltage source. Current is always leading the capacitor voltage by 90^o. If the source voltage has a constant amplitude value and its frequency is increased, the amplitude of the current increases accordingly. Further, when the frequency of the source decreases, the current amplitude decreases. Therefore, the capacitor offers opposition to current, which varies inversely with frequency.

Capacitive Reactance

The opposition to sinusoidal current in a capacitor is called capacitive reactance. The symbol is X_c, and its unit is the ohm. X_c varies inversely not only with frequency but with capacitance as well. When a sinusoidal voltage with a fixed amplitude and fixed frequency is applied to a capacitor with given value, there is a constant amount of AC current. When the capacitance value is increased, the current increases. The formula for X_c is shown above. Ohm's Law applies to capacitive circuits as follows: U = I X_c.

Universal motor

Design of Universal motor

Universal motors have two windings connected in series – the exciter winding and the armature winding. The rotor is designed as a laminated steel core. Several coils form the armature winding, whose winding turns are arranged in grooves located on the rotor surface. The ends of each coil are connected to the neighbouring collector segments. The stationary carbon brushes feed the coils with current one after the other as the rotor rotates. The stator is equipped with two salient poles which accommodate the exciter windings and is also built of laminated steel sheeting. To reduce power losses the windings can also be inserted into grooves.

How the motor operates

 

As the exciter winding and the armature winding are connected in series, the same current flows through them both, i.e. the magnetic fields in the stator and the armature are in phase. The magnetic fields situated perpendicular to each other cause torque to be exerted on the rotor of the motor – the north pole of the armature field is drawn by the south pole of the stator field and repelled by the north pole. The important thing here is that both fields do not rotate. The alternating current only causes the simultaneous direction reversal of the two magnetic fields. The direction of the torque exerted on the rotor remains unchanged.

Torque, speed and back emf

 

As long as the rotor has not been put into motion, the armature current is solely limited by the winding resistance. The torque is at its maximum and the motor's speed rapidly increases. Back emf is induced in the armature winding, which opposes the externally applied voltage in conformity with Lenz's law. The higher the rotor speed, the greater the back emf induced in the armature. As a result the current and thus the torque developed by the motor is diminished. An equilibrium comes about – the motor turns with a constant speed at which the torque being developed is adjusted to the load.

Operating response

 

In its design and the way it operates the universal motor is analogous to the series-wound motor. It has a very high starting torque. Its rotation speed can also be high and is variable over a wide range. Phase control allows for continuously adjustable speed/power control. The pole reversal of the stator or armature winding causes reversal of the rotation direction. Short-term overloads are not dangerous for these motors. However, when the load is so high that the motor comes to a standstill, there is a danger that the winding insulation may become damaged. At no-load the universal motor can end up "racing" which can lead to the destruction of the armature winding.

Applications

 

Single-Phase AC Motors

Motor types

 

 

In single-phase AC motors we distinguish between motors with commutators and induction motors. The series-wound motor for AC voltage is a motor with commutator – the current is supplied to the rotor via carbon brushes. In the case of motors with squirrel-cage rotors the electrical current is induced in the rotor. For that reason these kinds of motors are called induction motors.

Single-Phase Transformers

Type of Single-Phase Transformers

 

 

There are various types of single-phase transformers which have distinct structural design and electrical characteristics depending on their purpose. Bell transformers are the single-phase transformers most frequently used. Autotransformers, high-reactance transformers and welding transformers are examples of special transformers. Current and voltage transformers are used to connect up measuring instruments.

Transformers Design

 

A single-phase transformer consists of two electrically isolated windings which are mounted on a common core made of sheet steel. The individual sheets are mutually insulated with respect to each other and layered so that the abutting surfaces overlap. The windings are made of coating copper wiring which are wound onto a coil body made of plastic. The individual piles or layers are normally mutually insulated from each other by insulating foil. Essential transformer attributes include the shape of the iron core, the core's cross-section, the number of winding turns N1 and N2 for high voltage and the lower voltage winding, as well as the winding configuration.

How it works

 

Single-phase transformers transform single-phase AC into single-phase alternating current of the same frequency but with a different voltage. The way this works is simple – the electrical energy absorbed by the input winding is transferred to the iron core via the alternating magnetic flux. The alternating magnetic flux induces a voltage of the same frequency as the input voltage in the output winding. In an ideal transformer the output voltage's phase shift is 180° with respect to the input voltage.

Types of Capacitors

Capacitors are normally classified according to the type of dielectric material used. The most common types are mica, ceramic, plastic-film, and electrolytic (aluminum oxide, tantalum oxide) capacitors. Capacitors are also available as surface-mounted components. They are called chip capacitors.

Mica Capacitor

Ceramic Capacitor

Plastic-film Capacitor

Capacitor values are indicated on the capacitor body either by numerical or alphanumerical labels or sometimes by color code. Capacitor labels indicate various parameters such as capacitance, voltage rating, and tolerance.
The illustration shows the basic construction of mica, ceramic, and plastic-film capacitors.

Electrolytic Capacitors

Tantalum capacitors

  Aluminum Capacitor

Electrolytic capacitors offer much higher capacitance values than mica or ceramic capacitors and their voltage ratings are typically higher. Aluminum electrolytic capacitors are the most commonly used type. Tantalum capacitors have larger C, in smaller size, but they cost more than the aluminum type. Electrolytic capacitors are the only capacitors that require the observation of polarity when connecting to a circuit. Reversal of the voltage polarity can completely destroy a capacitor. The illustration shows typical electrolytic capacitors and a cut-away view of a teardrop-shaped tantalum capacitor.  

Variable Capacitors

Variable capacitors are used in a circuit where it is necessary to adjust the capacitance value, for example, in radio or TV tuners. The schematic symbol for a variable capacitor is shown above.

 

Adjustable capacitors that normally have slotted screw-type adjustments are called trimmers. They are used for very fine adjustments in a circuit. Ceramic or mica is a common dielectric in these capacitor types. Capacitance value is directly related to plate area A, and inversely related to plate separation d. For this reason, it is usually changed by adjusting one of these parameters.